设计师谈 |《数学之美》给我出的三道难题

所幸，这是一个网络时代。围绕四个表现内容，我分配了整个设计周期大约四分之三、二十多天的时间，通过网络科普，以及数学教学视频，来学习相关的数学基础知识，认识了几位伟大的数学家，了解了许多数学背后的故事。这是这套邮票设计最至关重要的部分。这个过程使我获益匪浅，使我隐约感受和找到了我理解之下的数学之美，它不太清晰但却足够震撼，这个关键词就是：优雅。不同于衣食住行、容貌气质这种外在的、日常和表面的优雅，数学的优雅是一种内在的、高级的优雅，是一种比这个词本身还要更高级的优雅。由此奠定了《数学之美》这套邮票设计的整体视觉基调。

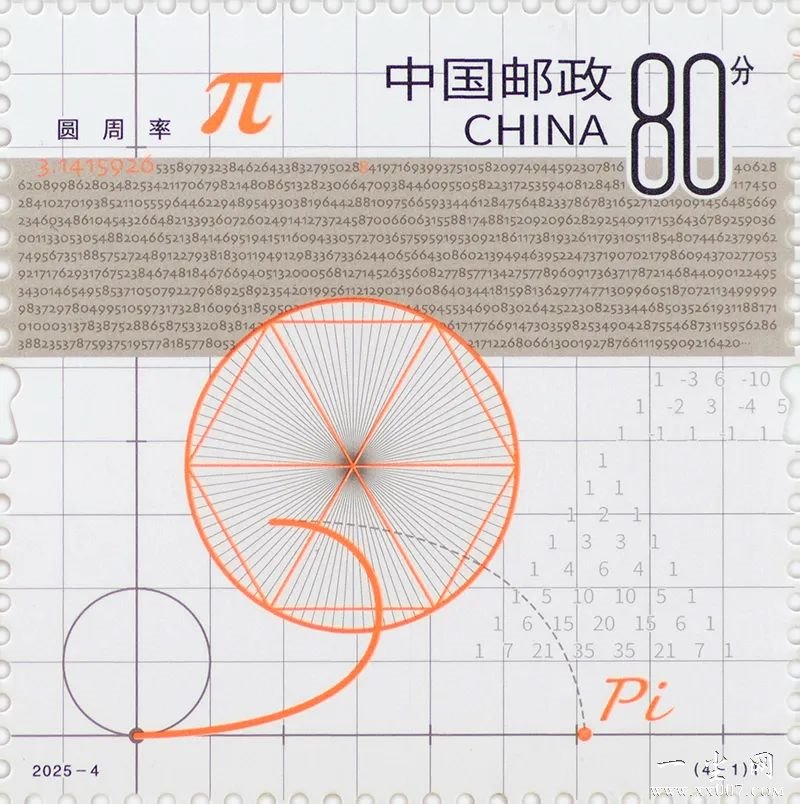
第一枚邮票表现了最重要的数学常数之一——π。藉由π值计算方法的演变，以小见大，体现了数学的发展是一个漫长而艰难，逐步深入而至豁然开朗、曲径通幽的过程。主体图形以图示的形式，组合表现了π的基本概念以及最古老的π值计算方法——割圆术。图中展示了将圆6等分和96等分切割时的情况，表明了这种方法的计算难度是呈几何级增长的。也解释了为何在此后的近1500年时间里，π值的精确度也仅仅来到了小数点后38位。这其中，我国古代伟大的数学家祖冲之最早将π值准确计算到3.1415926到3.1415927之间，这一数值被记录在唐代史书——《隋书》中。设计时，特意将这一数值放大标红处理，将《隋书》书影作为大版边饰，以纪念这一伟大的数学成就。时间来到17世纪后期，大名鼎鼎的科学家牛顿，在对二项式定理以及杨辉三角的研究中，结合刚刚发明不久的微积分，意外找到了计算π值的新方法，使得计算效率大幅度提升。直到现在，在计算机的帮助下，使用牛顿的方法让我们已经可以将π值计算到小数点后万亿位。因此，在画面内还特别表现了杨辉三角，用无色荧光表现了微积分符号。并以微缩文字的方式，记录了π值小数点后996位的准确数值。（设计初衷为微缩1000位，由于四舍五入的规则，出于严谨准确的考虑，舍去后4位。）

此外，德国数学家鲁道夫也是让我颇为感动的数学家。他用尽半生的时间，直到去世，使π值来到了第35位。并将这一数值铭刻在墓碑之上。这种精神不仅是数学研究最基础、最宝贵的精神，更是与国家所提倡的“大国工匠”精神异曲同工、不谋而合。所以将第35位标红以记之。

第二枚邮票对于勾股定理的表现包含两层含义。一是表现了数学在人们实际生活生产中的广泛应用。另一层含义为：数学作为最基础的科学，不论地域与时空，它是人类基于生产实践所得到的共同发现与思考。画面中，除了以三层结构，动态的展示了勾股定理完整的论证推导方法之一，同时还展示了《周髀算经》中周王与商高的对话（勾三股四玄五即出于此），以及关于“陈子测日”的记载。展示了古埃及和古印度结绳以计算的古老数学应用，直到现代科技中的GPS定位，其根本原理亦为勾股定理。由此可见，无论是古代还是现代，无论是东方文明，还是西方文明，整个人类在不同的时空之下，在不同环境之中，不约而同的发现和总结出相同的数学规律，并广泛应用。这真是一件不可思议，令人赞叹的事情。

第三枚邮票是对伟大数学家的致敬。欧拉公式是全世界公认最优美的公式。它将自然常数e、虚数i、圆周率π、以及0和1，这五个数学中最重要、最基础，但看似毫无关联的常数，以极其简洁，极其优雅的方式组成了一个完美等式。并且这个等式在复平面坐标系内，在时间轴上对应了一条包含标准正、余弦曲线的螺旋线图形，从任何角度看，欧拉公式都是完美无瑕的。然而，更加令我为之动容，深深感动的是，“创造”这个最完美的公式的伟大数学家——欧拉，却是“不完美”的。他在28岁时，右眼已经因疾致盲，59岁双目失明。这位13岁便进入拉塞尔大学学习的伟大天才的许多开创性学术贡献，竟然是凭借其超强的心算能力和记忆力完成的，成为为这个世界留下最多科学成果的数学家和科学家。读一读欧拉生平，如我一样，你一定会被他的超强天赋和伟大贡献所折服！邮票背景以极限微缩的e、π、i、0、1五个字符，构成了欧拉画像的双眼特写，以此表达对于这位数学大师，最由衷的仰望。

第四枚邮票是关于数学与哲学的思考。莫比乌斯带是一个关于维度，简单但却非常神奇的数学模型。从小蚂蚁的视角来看，莫比乌斯带是一个二维的平面，笔直且没有尽头。但是从人类的视角看来，小蚂蚁在三维空间内，在不翻越边缘的情况下，就走遍了莫比乌斯带的正反两面，无限循环。假设有朝一日，我们能够站在更高的维度去观察人类自身，人类是否就如同那只小小的蚂蚁一样，生活在我们所认为的无边无际的宇宙之中？三维结构的莫比乌斯带——克莱因瓶，是否就是三维宇宙的真实样貌呢？这是通过对数学的研究，进而引发的富有哲学意味的思考。